Analyzing temperature data with Ariadne

by Evelina Gabasova

This FsLab journal shows an example usage of Ariadne, F# library for Gaussian process regression.

Let's say I want to know how the weather was over the last few weeks in Cambridge, UK. Of course, I can download historical data from the Open Weather Map and analyse them. But what if I do not trust the summary data they provide for cities? I want to go to the source and download actual data measured at individual weather stations. If I download historical data from several nearby locations, I should be able to get some idea about the weather in the area.

Open Weather Map provides all their data in Json format, which means I can use F# Data to access all the information. First, we need to open all the necessary namespaces. I will also use F# Charting to generate some figures.

1: 
2: 
3: 
4: 
5: 
6: 

#r "Ariadne.dll"
open Ariadne.GaussianProcess
open Ariadne.Kernels

open FSharp.Data
open FSharp.Charting

Now I can download data directly from Open Weather Map. I create a query which requests a specific number of weather stations which are closest to a specific location. Here I use Json type provider to load a list of 5 closest weather stations.

 1: 
 2: 
 3: 
 4: 
 5: 
 6: 
 7: 
 8: 
 9: 
10: 
11: 
12: 

// Json type provider 
type WeatherStations = JsonProvider<"http://api.openweathermap.org/data/2.5/station/find?lat=52.2&lon=0.12&cnt=5">

// Cambridge location
let latitude = 52.2
let longitude = 0.12
let count = 5

// load data from Open Weather Map
let query = @"http://api.openweathermap.org/data/2.5/station/find?lat=" 
            + string latitude + @"&lon=" + string longitude + "&cnt=" + string count
let stations = WeatherStations.Load(query)

We can also check how far are the weather stations from Cambridge. It seems that they all lie approximately within 15 miles from Cambridge.

1: 
2: 

stations 
|> Array.iter (fun station -> printfn "%.2f" (float station.Distance))

3.49
3.79
5.84
13.00
15.71

Now we send a query to Open Weather Map asking for historical data for each of the five weather stations. The constructed query should return summarized daily weather data approximately for the past month. Again, I am using Json type provider to access the data.

 1: 
 2: 
 3: 
 4: 
 5: 
 6: 
 7: 
 8: 
 9: 
10: 

type StationData = JsonProvider<"http://api.openweathermap.org/data/2.5/history/station?id=51473">

let stationIds = stations |> Array.map (fun station -> station.Station.Id)

let stationQuery (station:int) = 
    @"http://api.openweathermap.org/data/2.5/history/station?id=" + string station

let stationData = 
    stationIds
    |> Array.map (fun id -> StationData.Load(stationQuery id))

After this step, we should have all the historical data for each station in stationData. I am interested in temperatures over the past month, so I extract only the average temperatures for each day. In general, station data contain also other information like atmospheric pressure, precipitation or wind speed. In the following code, I extract the temperature in Celsius, and return it together with its corresponding time of measurement.

 1: 
 2: 
 3: 
 4: 
 5: 
 6: 
 7: 
 8: 
 9: 
10: 
11: 
12: 
13: 

// Extract temperatures
let temperatures = 
    stationData
    |> Array.map (fun s ->
        s.List |> Array.map (fun dt -> 
           // raw temperatures are in Kelvin, transform to Celsius
           dt.Dt , (float dt.Temp.V) - 273.15))

// Plot temperature data
temperatures
|> Array.map (fun ts -> Chart.Point(ts, MarkerSize=10))
|> Chart.Combine
|> Chart.WithYAxis(Min=10.0, Max=25.0)

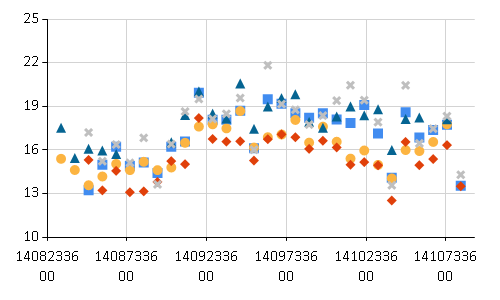
Notice that the data are quite noisy. Also, we have different number of observations from different weather stations. Each day, sometimes there are 5 observations, sometimes only 2, sometimes there are outliers. Gaussian processes are a great tool to model this form of data because they take all the noise and uncertainty into account.

Another thing to notice is that Open Weather Map provides all date and time information in unix time. To bring all the time into a more interpretable range, I change the scale into days. I also create an F# record containing Locations and Observations which is used by Ariadne to pass data into Gaussian process.

 1: 
 2: 
 3: 
 4: 
 5: 
 6: 
 7: 
 8: 
 9: 
10: 
11: 

let startTime = 
    temperatures |> Array.map (fun ts -> Array.minBy fst ts |> fst)
    |> Array.min

let data = 
    temperatures
    |> Array.map (fun temps ->
        {Locations = 
            Array.map (fun (t,_) -> 
                float (t - startTime) / (24.0 * 3600.0)) temps
         Observations = Array.map snd temps})

Now we can construct a Gaussian process with squared exponential covariance function. Squared exponential kernel generally characterizes very smooth functions.

1: 
2: 
3: 
4: 
5: 

let lengthscale = 1.0
let signalVariance = 20.0
let noiseVariance = 1.0

let sqExp = SquaredExp.SquaredExp(lengthscale, signalVariance, noiseVariance)

I guessed some values for hyperparameters of the squared exponential covariance function. The first hyperparameter is the lengthscale. Its value regulates how quickly the function values change, how wide squiggles we expect to see in the function. Lengthscale of 1 assumes that the temperature changes quite quickly from day to day.

The second parameter is the signal variance which regulates how far does the function go from its prior mean. Since the prior mean function of our Gaussian process is zero and I am being lazy by leaving the data on their original scale, I have to set quite a large variance. The last parameter is the noise variance which models the amount of noise present in the observed data. You can find more details on interpretation of each hyperparameter in the documentation.

With hyperparameters prepared, we can finally fit the Gaussian process regression model.

1: 
2: 

let gp = sqExp.GaussianProcess()
gp |> plot data

The graph shows the mean estimated temperature as a blue line. The grey region corresponds to a 95% confidence interval. The fit is quite good, the confidence interval captures most of the observed data and the mean captures the general trend. You can see that the function goes to zero rapidly outside of the observed region. This is because the Gaussian process prediction reverts to the prior mean value when there are no observations. Note that the confidence interval is also getting much wider. Generally we can reliably extrapolate only about one lengthscale outside of the data regions.

Optimizing hyperparameters

Guessing values hyperparameters is not a very reliable method of fitting a model. Ariadne provides two basic methods for optimizing hyperparameters:

• Metropolis-Hastings posterior sampling
• simple gradient descent

Both methods are optimizing the log likelihood of the hyperparameters given observed data. The first method, Metropolis-Hastings, is a probabilistic method which gives us the mean estimate of the posterior distribution given observations and our prior beliefs about hyperparameter values. This is the proper Bayesian method for optimizing hyperparameters.

First we need to set prior distributions for each hyperparameter. Here I am using a Log-normal prior because all hyperparamters have to be larger than zero. The prior distributions are centred around my initial guessed values.

 1: 
 2: 
 3: 
 4: 
 5: 
 6: 
 7: 
 8: 
 9: 
10: 
11: 
12: 
13: 
14: 
15: 
16: 

open MathNet.Numerics
open Ariadne.Optimization
open Ariadne.Optimization.MetropolisHastings

let rnd = System.Random(0)
let lengthscalePrior = Distributions.LogNormal.WithMeanVariance(1.0, 1.0, rnd)
let variancePrior = Distributions.LogNormal.WithMeanVariance(20.0, 5.0, rnd)
let noisePrior = Distributions.LogNormal.WithMeanVariance(0.5, 1.0, rnd)
// construct the prior distribution
let prior = SquaredExp.Prior(lengthscalePrior, variancePrior, noisePrior)

// set parameters for Metropolis-Hastings sampler
let settings = 
    { Burnin = 500       // Number of burn-in iterations
      Lag = 5            // Thinning of posterior samples
      SampleSize = 100 } // Number of thinned posterior samples

Metropolis-Hastings sampler in Ariadne samples from the posterior distribution and returns the mean estimate for each hyperparameter.

1: 
2: 
3: 
4: 
5: 
6: 
7: 

// Run the sampler
let kernelMH = SquaredExp.optimizeMetropolis data settings prior sqExp
// Construct updated Gaussian process
let gpMH = kernelMH.GaussianProcess()

gpMH |> plot data
|> Chart.WithXAxis(Min=0.0, Max = 30.0)

1: 
2: 

printfn "Original Gaussian process likelihood: %f" (gp.LogLikelihood data)
printfn "MH Gaussian process likelihood: %f" (gpMH.LogLikelihood data)

Original Gaussian process likelihood: -333.369341
MH Gaussian process likelihood: -246.006847

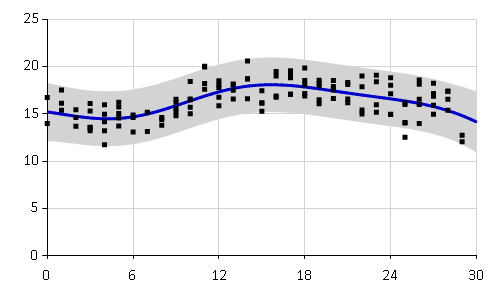
Log likelihood of the new Gaussian process increased quite significantly, which means that the optimized Gaussian process provides a much better fit to the observed training data than the original one.

The second option how to select values of hyperparameters is standard nonlinear optimization. Ariadne currently implements only basic gradient descent algorithm. This method uses derivatives of the log likelihood function to find a local optimum.

 1: 
 2: 
 3: 
 4: 
 5: 
 6: 
 7: 
 8: 
 9: 
10: 
11: 
12: 
13: 
14: 

let gdSettings = 
    { GradientDescent.Iterations = 1000; 
      GradientDescent.StepSize = 0.1}
let gradientFunction parameters = SquaredExp.fullGradient data parameters

// Run gradient descent
let kernelGD = 
    gradientDescent gradientFunction gdSettings (sqExp.Parameters)
    |> SquaredExp.ofParameters

// Create optimized Gaussian process
let gpGD = kernelGD.GaussianProcess()

gpGD |> plotRange (0.0, 30.0) data

1: 
2: 

printfn "Original Gaussian process likelihood: %f" (gp.LogLikelihood data)
printfn "GD Gaussian process likelihood: %f" (gpGD.LogLikelihood data)

Original Gaussian process likelihood: -333.369341
GD Gaussian process likelihood: -241.782424

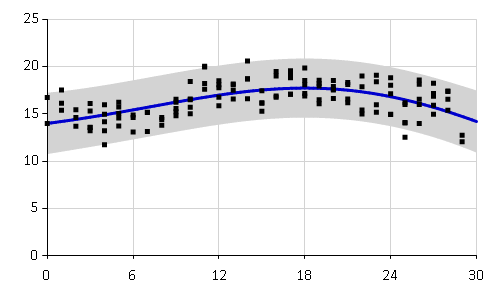
Gradient descent found different optimum than Metropolis-Hastings. The fit seems to capture mainly the overall trend in the temperatures over the whole month.

The two methods generally yield different resulting models. Metropolis-Hastings takes into account our prior beliefs about hyperparameter values and it also samples from the true posterior. Gradient descent finds only a single local maximum of the nonlinear log likelihood function.

You can download the fsx source file for weather analysis from GitHub.