Getting started: Simple regression with Ariadne

This tutorial shows how to use the Ariadne library for Gaussian process regression.

As a first step, we need to get Ariadne.dll from NuGet. Then we can load the Ariadne library inside F#.

1: 
2: 
3: 

#r "Ariadne.dll"
open Ariadne.GaussianProcess
open Ariadne.Kernels

We will introduce Ariadne through a practical example. Consider a time series dataset with missing values. For example, we might be interested in income distribution and inequality in Russia over the past 30 years. We can download available data from the World Bank using FSharp.Data library. We will use FSharp.Charting to display the data. We will also need a reference to Math.NET Numerics.

 1: 
 2: 
 3: 
 4: 
 5: 
 6: 
 7: 
 8: 
 9: 
10: 
11: 
12: 
13: 
14: 

#r "FSharp.Data.dll"
#r "FSharp.Charting.dll"
#r "MathNet.Numerics.dll"

open FSharp.Data
open FSharp.Charting

let wb = WorldBankData.GetDataContext()

let rawData = 
    wb.Countries.``Russian Federation``.Indicators.``GINI index`` 
    |> Seq.toArray

Chart.Point(rawData)

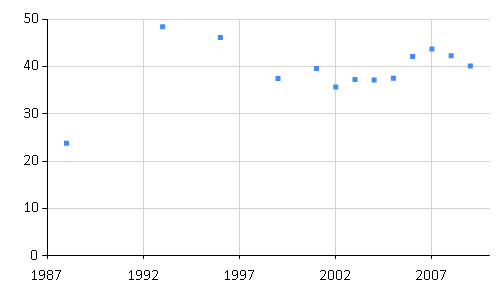
The snippet downloads raw data from the World Bank on the Gini index, which measures income inequality. We can see that the time series contains missing data, for example there are no values between years 1988 and 1993.

[|(1988, 23.8); (1993, 48.38); (1996, 46.11); (1999, 37.48); (2001, 39.6);
  (2002, 35.7); (2003, 37.26); (2004, 37.14); (2005, 37.51); (2006, 42.13);
  (2007, 43.71); (2008, 42.27); (2009, 40.11)|]

We can use Gaussian process regression model to interpolate the observed data and estimate Gini index in the years when it was not measured. As a first step, we need to prepare the downloaded data.

Data preprocessing

 1: 
 2: 
 3: 
 4: 
 5: 
 6: 
 7: 
 8: 
 9: 
10: 
11: 

let years, values = Array.unzip rawData

// inputs
let xs = years |> Array.map float   
// centred outputs
let ys = 
    let avg = Array.average values
    values |> Array.map (fun y -> y - avg)

// Gaussian process data
let data = [{Locations = xs; Observations = ys}]

We formulated the data in the form expected by the Gaussian process library. General data for Gaussian process consist of a sequence of series measurements. In our case, we have only one time series. Each series of measurements contains locations of each measurement (time points in our example) and observed values for each location (Gini index values). The Locations and Observations arrays should have equal length.

In general applications, locations and observations are not restricted to time series. For example locations can represent geographical coordinates and observations might record rainfall at each location.

Covariance function

Covariance functions (also called kernels) are the key ingredient in using Gaussian processes. They encode all assumptions about the form of function that we are modelling. In general, covariance represents some form of distance or similarity. Consider two input points (locations) \(x_i\) and \(x_j\) with corresponding observed values \(y_i\) and \(y_j\). If the inputs \(x_i\) and \(x_j\) are close to each other, we generally expect that \(y_i\) and \(y_j\) will be close as well. This measure of similarity is embedded in the covariance function.

Ariadne currently contains implementation of the most commonly used covariance function, the squared exponential kernel. For more information see Covariance functions. The following snippet creates the squared exponential covariance function.

1: 
2: 
3: 
4: 
5: 
6: 

// hyperparameters
let lengthscale = 3.0
let signalVariance = 15.0
let noiseVariance = 1.0

let sqExp = SquaredExp.SquaredExp(lengthscale, signalVariance, noiseVariance)

The hyperparameters regulate specific behaviour of the squared exponential kernel. For details see the Covariance functions section. Details on how to select values for hyperparameters are in the Optimization section of this website.

Gaussian process regression

There are two ways how to create a Gaussian process model. The first one uses directly the squared exponential kernel that we created in the previous snippet. The second option is to create Gaussian process model 'from scratch' by specifying a covariance function, prior mean and optional noise variance. The library currently implements only zero prior mean.

1: 
2: 
3: 
4: 
5: 
6: 

// First option how to create a Gaussian process model
let gp = sqExp.GaussianProcess()

// Second option how to create a Gaussian process model
let covFun = sqExp.Kernel
let gp1 = GaussianProcess(covFun, ZeroMean, Some noiseVariance)

Now that we created a Gaussian process, we can use it to compute regression function. Please note that current implementation of inference in Gaussian processes is exact and therefore requires \(\mathcal{O} (N^3)\) time, where \(N\) is the number of data points.

We can compute log likelihood to see how well the Gaussian process model fits our World bank data. The log likelihood may be used to compare different models.

1: 

let loglik = gp.LogLikelihood data

-45.09576717

We can also use Gaussian process to estimate values of the Gini index in years where there are no data. The Predict function gives us the mean estimate for each time location and variance of the estimate.

1: 
2: 
3: 
4: 
5: 
6: 
7: 

let allYears = [| 1985.0 .. 2015.0 |]
let predictValues, predictVariance = allYears |> gp.Predict data

Array.zip3 allYears predictValues predictVariance
|> Array.iteri (fun i (year, gini, var) -> 
    if i < 5 then
        printfn "%.0f : %.3f (+/- %.3f)" year gini (sqrt var)) 

We can print the predicted values for each year together with their standard deviations.

1985 : -10.091 (+/- 3.250)
1986 : -13.017 (+/- 2.585)
1987 : -14.740 (+/- 1.808)
1988 : -14.381 (+/- 1.390)
1989 : -11.567 (+/- 1.655)

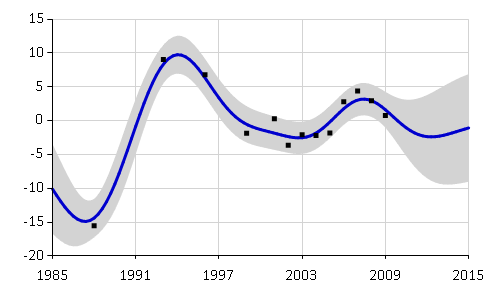
To display the full posterior regression function, we can also automatically plot the Gaussian process using F# Charting. There are two functions for Gaussian process charts included in the library. There is a basic plot function, which uses Gaussian process to interpolate observed values. The plotRange function extrapolates the Gaussian process over a specified range of values. We can use it to draw a graph of estimated Gini index values between years 1995 to 2015.

1: 

gp |> plotRange (1985.0, 2015.0) data

Continue to Covariance functions to find out more about the squared exponential covariance. Optimization provides an overview of how to fit hyperparameters of covariance functions (lengthscale, signal variance etc).

• Ariadne
• Home page
• Get Library via NuGet
• Source Code on GitHub
• License
• Release Notes
• Getting started
• Tutorial
• Covariance functions
• Optimization
• Quick how-to
• Example: Modeling temperatures
• Documentation
• API Reference